
原始文明的“核甘地”的傳說是遊戲界最著名的蟲子之一,但是它是如何工作的,甚至是真實的?繼續閱讀以了解有關傳說中的核Gandhi錯誤及其歷史的更多信息。
←返回Sid Meier的文明VII主文章
Civ 7不會讓Gandhi去核能,但是他曾經嗎?

每個遊戲社區都有自己的神話 - 在玩家之間竊竊私語,謠言像民俗一樣傳遞。如今,像Herobrine和Ben之類的名字在Gaming最令人寒冷的城市傳奇方面佔據了對話。但是在早期,當視頻遊戲變得更簡單,主流越來越少時,每當出現神話和小故障的話題時,玩家的腦海中就會大致隱約可見:核甘地。
即使是現代文明粉絲也可能不認識的名字,但曾經是傳奇人物中的傳奇人物。據這個故事說,第一場文明遊戲是一個奇異的蟲子的家園,它使著名的和平的印度領導人變成了一個無所適從的溫暖者,隨時準備在敵人身上向敵人大火。聽起來很有趣,而且令人恐懼,這聽起來有什麼道理嗎?還是核甘地只是社區想像力瘋狂的另一個案例?讓我們找出答案。
核甘地的傳說是首先知道的
在深入研究事實之前,讓我們從傳奇本身開始。這個故事說,在遊戲的AI控制時,MS-DOS原始文明遊戲中的領導者俱有侵略性參數。該參數範圍從1到10,或者在某些帳戶中為1至12,其中1個是和平主義者,而10個是一個全面的溫暖者。
由於莫漢斯·甘地(Mohandas Gandhi)是一個和平主義者,因此他的領導人AI的侵略默認為1。在大部分比賽的大部分時間裡,甘地都會像其他任何領導人一樣行事,但是在中部比賽中,一旦他採用民主作為政府,他的侵略水平就會下降2。這使他的侵略參數在-1處。
這是傳說中最重要的部分所在的地方:據稱,該侵略參數被存儲為8位無簽名的整數變量,其範圍為0到255。甘地的負面侵略水平,顯然是導致整數溢出,並在最小的價值上封頂,而不是在255次範圍內被限制為255。 遊戲。
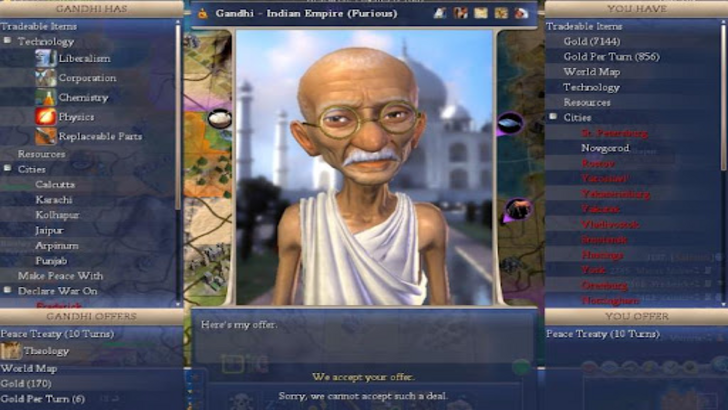
現在,提出這樣的事實,即核武器在採用民主之後就可以使用,而您已經有了混亂的秘訣。然後,甘地將開始彈奏彈頭,轉彎後在其他文明中發射它們,同時成為他在現實生活中的和平主義者的同一位領袖。因此,這個版本的甘地獲得了臭名昭著的核甘地頭銜。
整個社區的核蔓延

核甘地存在的消息像野火一樣在文明社區中蔓延開來,在引起整個遊戲世界的關注之前,迅速點燃了更廣泛的4x場景。您可能會認為這個傳奇與遊戲的發行伴隨著,在鼎盛時期獲得了吸引力,但沒有。儘管文明一直在1991年首次亮相,但直到2010年代中期,核甘地才真正爆炸。
到那時,文明V已經在現場,原始文明的玩家群實際上不存在。驗證核甘地背後的真相幾乎是不可能的,而且遊戲已經將近二十年了,很容易假設神話來自編碼和軟件限制。但是,正如游戲的設計師後來澄清的那樣,完全不是這種情況。
西德·梅爾(Sid Meier)確認核甘地是不可能的
“不可能的。”這就是Sid Meier這個詞(原始文明的設計師和整個系列的同名人物)在遊戲發行後近30年,在傳奇紮根近十年後,在2020年描述了核甘地。
根據邁耶(Meier)的說法,由於與遊戲的實際設計有兩個關鍵的不一致,核甘地的概念從一開始就存在缺陷。首先,所有整數變量默認情況下簽名,這意味著-1首先不會導致溢出值。其次,政府類型根本沒有影響侵略水平,因此在整個比賽中,甘地的行為保持不變。

文明II的首席設計師布萊恩·雷諾茲(Brian Reynolds)支持了這一點,並解釋說,原始遊戲只有三個可能的侵略水平,甘地與該遊戲領導者的三分之一分享了他的和平主義者的環境。即使有可能的核甘地,他也不是唯一成為流氓的領導人。最重要的是,代碼的相關部分沒有未簽名的變量,即使領導者以某種方式超過了最大侵略參數,也沒有任何編碼可以使它們更加積極地行動。
最後,核甘地的傳說不過是……一個傳奇。真理的捏造,傳播到未來。但是,儘管如此,但不可否認,它對社區的未來幾年產生了影響。
核甘地如何成為(兩次)
儘管被徹底揭穿了核能,但核甘地仍然是遊戲最臭名昭著的“蟲子”之一,這很可能是因為它的諷刺性太完美了,無法忽略。實際上,在2012年之前沒有提到這樣的小故障,當時用戶在電視比喻的文明頁面上添加了一個神話般的錯誤。從那裡開始,遊戲出版物就探討了這個故事,不久之後,傳奇人物奪走了自己的生活。
那麼,為什麼有人會發明關於幾十年前發布的遊戲的神話,又如何傳播這麼快?簡短的答案:這不是一個神話。儘管最初的文明從未有過核甘地,但文明V絕對做到了。儘管是比賽中最和平的領導者,但甘地的AI被明確編碼,以建立和推出核武器可能具有最高的偏好 - 這項決定由遊戲的首席設計師喬恩·謝弗(Jon Shafer)確認並親自實施。

儘管Civ V的Gandhi和電視比喻上的偽經蟲帖子之間沒有直接的聯繫,但時間表表明這是傳奇人物像Wildfire一樣在傳播之前首次紮根的地方。
最後,核甘地不是真實的,至少不是描述的神話 - 但他確實存在。
文明VI甚至通過給甘地有70%的機會來製定“核武器快樂”的隱藏議程,從而傾向於開玩笑。至於文明vii,甘地這次不在陣容中,這意味著核甘地的傳奇可能最終可以安息。但是,如果歷史教會了我們任何東西,那就是有些神話永遠不會真正死亡。
←返回Sid Meier的文明VII主文章
西德·梅爾(Sid Meier)的文明vii類似遊戲
















